Sanırım artık benim zamanım geldi de biraz geçiyor. Mikrofonu alma sırası bende ve bu gönderide beraber Logical Circuits e giriş yapmış olacağız.
Başlangıç olarak kitapların ve hocaların gittiği şekilde gidelim.
Sonsuz sayıda ara değer alabilen büyüklüğe analog büyüklük deriz. Giriş ve çıkış işaretlerinin birbirine benzediği devreye ise analog sistem deriz.
Analog sistemin dışında birde sayısal büyüklük ve sayısal sistemimiz vardır. Analogdan farklı olarak sayısal büyüklük yalnızca iki değer alabilir (Buna var-yok, açık-kapalı, 1-0 vb. diyebiliriz). Sayısal büyüklüğü göstermek için kullandığımız 1 ve 0 gibi iki değer alabilen işarete de sayısal işaret deriz.
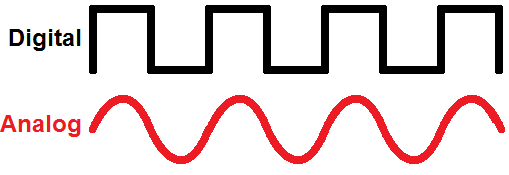 |
| Analog vs. Digital (Sayısal) Analogda ikiden fazla değer varken dijitalde yalnızca iki değer mevcuttur. |
Analog sistemi kavramak açısından bir örnek verelim. Bir şarkıcı şarkısını söylemeye başladığında analog dalgalar üretir. Ancak şarkıcının sesini bilgisayara kaydetmek istediğimizde analog dalgayı dijital dalgaya çevirmemiz gerekir ve tüm ses 1 ve 0 lar (ya da var ya da yoklar) ile bilgisayarımızda kayıt olmaktadır. Sanatçının sesi aralıksızdır bu yüzden analogdur.
Ancak şarkıyı tekrar bir ses kaynağından çalarsak bu sefer de dijital olarak saklanmış sesimiz analoga çevrilerek ses kaynağından dışarı çıkacaktır.
Analog dalgada, dalga üzerinde ki herhangi küçük bir değişikliği bile gözlemlememiz mümkündür ancak dijital için bunu söyleyemeyiz. Çünkü dijitalde ya vardır ya yoktur. Eğer dijitalde belirlediğimiz frekans aralığımıza göre ne kadar ayrıntıyı görebileceğimizi seçeriz. Bunu aşağıdaki şeklimize bakarak daha iyi anlayabiliriz.
 |
| Büyütmek için üzerine tıklayınız |
Bu şekilde bir giriş yaptıktan sonra kullanılan sayı sistemlerimize ilk adımımızı atalım.
Günlük hayatımızda 10 tabanında sayılar kullanırız. Ancak aslında tek sayı sistemi 10 tabanlı (decimal) sayı sistemi değildir. Onluğa ek olarak; ikilik (binary), sekizli (oktal) ve on altılı (heksadecimal) sayı sistemleri genellikle elektronik ve bilgisayar bilirimleri alanlarında yaygın olarak kullanılmaktadır.
| Decimal | Binary | Oktal | Heksadecimail |
|---|---|---|---|
00
|
00000
|
00
|
00
|
01
|
00001
|
01
|
01
|
02
|
00010
|
02
|
02
|
03
|
00011
|
03
|
03
|
04
|
00100
|
04
|
04
|
05
|
00101
|
05
|
05
|
06
|
00110
|
06
|
06
|
07
|
00111
|
07
|
07
|
08
|
01000
|
10
|
08
|
09
|
01001
|
11
|
09
|
10
|
01010
|
12
|
0A
|
11
|
01011
|
13
|
0B
|
12
|
01100
|
14
|
0C
|
13
|
01101
|
15
|
0D
|
14
|
01110
|
16
|
0E
|
15
|
01111
|
17
|
0F
|
16
|
10000
|
20
|
10
|
17
|
10001
|
21
|
11
|
18
|
10010
|
22
|
12
|
19
|
10011
|
23
|
13
|
20
|
10100
|
24
|
14
|
...
|
...
|
...
|
...
|
Sayı tablomuz bu şekilde. Peki çevirme işlemini nasıl yapacağımızı merak ediyorsanız cevabımız çok ama çok basit!
Mesela elimizde 2'lik tabanda 01011 sayısı var ve biz bunu decimal tabana çevirmek istiyoruz. Yapmamız gereken sağdan sola doğru sayılarımızı ikinin katları ile çarpıp en son olarak toplamak. Yani;
(0 x 24)+(1 x 23)+(0 x 22)+(1 x 21)+(1 x 20) = 11
Sonucunu elde etmiş olacağız.
Decimal bir sayıyı binary bir sayıya çevirmek içinse decimal sayıyı sürekli olarak ikiye bölüp, son bölme işlemindeki "bölüm" ü başa yazıp daha sonrasında sırası ile sağdan sola tüm kalanları yazarak istediğimiz sayıyı elde ederiz.
 |
| Resmi büyütmek için üstüne tıklayın |
Aynı mantığı kullanarak 10'luk tabanda ki bir sayıyı 8'e bölerek oktal, 16'ya bölerek de heksadecimal karşılığını bulabiliriz. Unutmamamız gereken nokta Heksadecimal sayı sistemi ekstra olarak A,B,C,D,E ve F içerir ve sırasıyla onluk tabanda 10, 11, 12, 13, 14 ve 15 e karşılık gelmektedir.
 | |
|
İyi çalışmalar,
Fettucini

Hiç yorum yok:
Yorum Gönder